"It’s just adding two numbers. How hard can it be?"
This is the deceptive promise that draws countless developers into a false sense of security. The problem statement seems child-like: you’re given an array and a target, find two indices whose values sum to that target. There’s even a candy-store analogy: imagine a shelf full of jars and a budget of $10; you need to pick two candies whose prices add up to $10. It’s easy to produce a solution that works on paper, but the real challenge is finding one that scales beyond toy examples.
The Complexity Explosion: O(n²) vs. O(n)
At first glance, a brute-force solution seems obvious: iterate over every possible pair of elements and return the first pair whose sum equals the target. For a small array, this works fine, but as the input grows, the running time explodes. A simple nested loop makes n² comparisons. In contrast, a more sophisticated approach uses a hash table (a dictionary in Python or HashMap in Java) to record seen values. As you iterate, you compute the complement target – num and check whether it already exists; this reduces the time complexity to O(n) and the space complexity also to O(n).
Feature comparison
The key differences between these two strategies can be summarized succinctly:
| Feature | Brute force | Hash-based |
|---|---|---|
| Time complexity | O(n²) nested loops | O(n) single pass |
| Space usage | O(1) (no additional structure) | O(n) for dictionary |
| Early exit | Possible when a pair is found | Possible when complement exists |
| Suitability | Small inputs, quick prototype | Large inputs, production use |
Visualizing the growth
To appreciate how quickly the brute-force approach becomes untenable, consider the logarithmic plot below. It compares the relative number of operations required by the two algorithms as the input size doubles. The steep blue curve corresponds to the quadratic brute-force solution while the orange curve shows the linear hash-based approach.
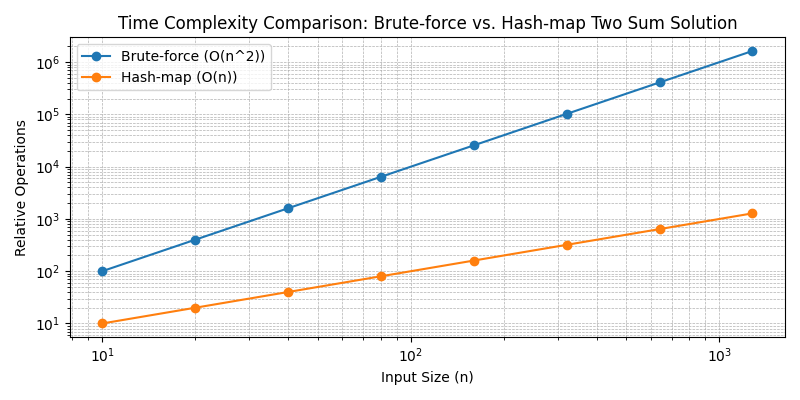
Notice that with small inputs, the difference is modest, but by the time n reaches a few hundred, the brute-force curve shoots upward while the hash-based curve grows much more gently. That’s why interviewers and production systems prefer the hash-table technique: it scales.
Anatomy of a Production-Ready Solution
Just like building a chat system isn’t just about “sending messages back and forth”, solving Two Sum for real workloads isn’t just about writing a quick loop. You need to account for edge cases and data structures. Below we break down two common approaches.
1. Brute-force enumeration
The brute-force method examines every unordered pair. In Python it looks like this:
def two_sum_brute_force(nums, target):
"""Return indices of the first pair summing to target. O(n**2) time."""
n = len(nums)
for i in range(n):
for j in range(i + 1, n):
if nums[i] + nums[j] == target:
return [i, j]
return None
This solution is easy to reason about, but its double loop makes it unsuitable for large input sizes. It also lacks immediate early termination when processing huge arrays since it still has to inspect all possible pairs.
2. Single-pass hash lookup
The hash-based algorithm keeps track of previously seen numbers and their indices. As you iterate through the array, you compute the complement target – num and check whether it already exists in the dictionary. Educative describes the steps as:
- Start with an empty dictionary to store numbers and their indices.
- For each number, compute its complement (
target – num). - If the complement is in the dictionary, you’ve found your pair and return the two indices.
- Otherwise, store the current number and index in the dictionary and continue.
Here’s the Python implementation:
def two_sum_hash(nums, target):
"""Return indices of two numbers that add up to target using a hash table."""
num_dict = {}
for i, num in enumerate(nums):
complement = target - num
if complement in num_dict:
return [num_dict[complement], i]
num_dict[num] = i
return None
In Java, the same idea leverages HashMap:
import java.util.HashMap;
import java.util.Map;
public class TwoSum {
public static int[] twoSum(int[] nums, int target) {
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
int complement = target - nums[i];
if (map.containsKey(complement)) {
return new int[]{map.get(complement), i};
}
map.put(nums[i], i);
}
return null; // no solution
}
}
This single-pass algorithm achieves O(n) time by trading space for speed. It’s exactly the pattern recommended in many tutorials because it handles large arrays gracefully and stops as soon as a valid pair is found.
Analogies: Keys and Locks
If the candy-shop story doesn’t resonate, imagine you’re at a key-maker’s workshop. Each number in nums is a key cut to a specific depth, and the target is a lock that requires two keys inserted together to open. When you pick up a key, you look for its matching counterpart (the complement). A brutish approach would try every possible pair of keys until you succeed. The more efficient locksmith has a pegboard labelled with the depth of each key; as soon as a new key arrives, he checks if the complementary depth is already hanging on the board. This pegboard is your dictionary or HashMap.

The diagram above captures the moment when two pieces fit together to produce the target. Think of the glowing pieces as keys found by the algorithm, slotting perfectly into the “lock” represented by the target.
Pitfalls and Edge Cases
As with any algorithm, there are gremlins lurking beneath the surface:
- Duplicate values: If the array contains the same number twice, the hash-based solution still works because it stores indices rather than values.
- Negative numbers: The problem statement often assumes positive numbers, but the hash-based approach handles negatives seamlessly because the dictionary only stores complements.
- No solution exists: Both approaches should return
None(ornullin Java) if no pair sums to the target. - Memory vs. speed trade-off: While O(n) time is attractive, the dictionary uses extra memory. In extremely memory-constrained environments you might still choose a two-pointer technique on a sorted copy, trading simplicity for in-place memory.
The Final Principle
The Two Sum problem teaches a universal lesson that applies far beyond this single interview question:
Design for the data structure, not the obvious loop. By modelling the state (a mapping of seen numbers to indices) instead of naively iterating through every pair, you gain orders-of-magnitude performance improvements. Use specialized structures—like dictionaries and hash maps—when appropriate, and remember that the simplest idea isn’t always the most scalable.
Armed with this deeper understanding, you’ll see how even the simplest problems can have layers of nuance. The next time someone says “it’s just adding two numbers”, you’ll know better.